40. Avancerade geometriska konstruktioner¶

Lagret nyc_subway_stations har gett oss många intressanta exempel hittills, men det finns något slående med det:

Även om det är en databas med alla stationer, tillåter det inte enkel visualisering av rutter! I det här kapitlet kommer vi att använda avancerade funktioner i PostgreSQL och PostGIS för att bygga upp ett nytt linjärt ruttskikt från punktskiktet för tunnelbanestationer.

Vår uppgift försvåras särskilt av två saker:

Kolumnen routes i nyc_subway_stations har flera ruttidentifierare i varje rad, så en station som kan förekomma i flera rutter visas bara en gång i tabellen.
I likhet med föregående fråga finns det ingen information om ruttordning i stationstabellen, så även om det är möjligt att hitta alla stationer på en viss rutt är det inte möjligt att använda attributen för att avgöra i vilken ordning tågen passerar stationerna.

Det andra problemet är svårare: hur ordnar vi en oordnad uppsättning punkter i en rutt så att de stämmer överens med den faktiska rutten.

Här är hållplatserna för ”Q”-tåget:

SELECT s.gid, s.geom
FROM nyc_subway_stations s
WHERE (strpos(s.routes, 'Q') <> 0);

På den här bilden är hållplatserna märkta med sin unika primärnyckel ”gid”.

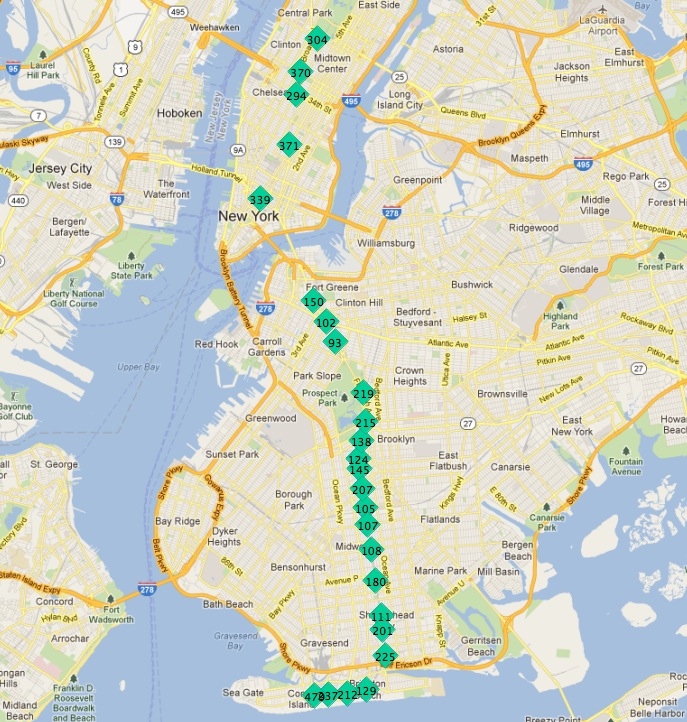
Om vi börjar på en av slutstationerna verkar nästa station på linjen alltid vara den närmaste. Vi kan upprepa processen varje gång så länge vi utesluter alla tidigare funna stationer från vår sökning.

Det finns två sätt att köra en sådan iterativ rutin i en databas:

Använda ett procedurspråk, som PL/PgSQL.
Använda rekursiva gemensamma tabelluttryck.

Common table expressions (CTE) har den fördelen att de inte kräver någon funktionsdefinition för att köras. Här är CTE för att beräkna rutten för Q-tåget, med början från den nordligaste hållplatsen (där gid är 304).

WITH RECURSIVE next_stop(geom, idlist) AS (
    (SELECT
      geom,
      ARRAY[gid] AS idlist
    FROM nyc_subway_stations
    WHERE gid = 304)
    UNION ALL
    (SELECT
      s.geom,
      array_append(n.idlist, s.gid) AS idlist
    FROM nyc_subway_stations s, next_stop n
    WHERE strpos(s.routes, 'Q') != 0
    AND NOT n.idlist @> ARRAY[s.gid]
    ORDER BY ST_Distance(n.geom, s.geom) ASC
    LIMIT 1)
)
SELECT geom, idlist FROM next_stop;

CTE består av två halvor som är sammanfogade:

Den första halvan etablerar en startpunkt för uttrycket. Vi får den initiala geometrin och initierar matrisen med besökta identifierare, med hjälp av posten ”gid” 304 (slutet av raden).
Den andra halvan itererar tills den inte hittar några fler poster. Vid varje iteration tar den in värdet från föregående iteration via självreferensen till ”next_stop”. Vi söker efter varje hållplats på Q-linjen (strpos(s.routes,’Q’)) som vi inte redan har lagt till i vår besökslista (NOT n.idlist @> ARRAY[s.gid]) och ordnar dem efter deras avstånd från föregående punkt, och tar bara den första (den närmaste).

Utöver den rekursiva CTE i sig finns det ett antal avancerade PostgreSQL-arrayfunktioner som används här:

Vi använder ARRAY! PostgreSQL stöder matriser av alla typer. I det här fallet har vi en matris av heltal, men vi kan också bygga en matris av geometrier eller någon annan PostgreSQL-typ.
Vi använder array_append för att bygga upp vår array av besökta identifierare.
Vi använder operatorn @> array (”array contains”) för att ta reda på vilken av Q-tågstationerna vi redan har besökt. Operatorn @> kräver ARRAY-värden på båda sidor, så vi måste omvandla de enskilda ”gid”-numren till arrayer med en enda post med hjälp av ARRAY[]-syntaxen.

När du kör frågan får du varje geometri i den ordning den hittas (vilket är ruttordningen), samt listan över identifierare som redan har besökts. Genom att paketera geometrierna i PostGIS ST_MakeLine aggregatfunktion förvandlas uppsättningen geometrier till en enda linjär utdata, konstruerad i den angivna ordningen.

WITH RECURSIVE next_stop(geom, idlist) AS (
    (SELECT
      geom,
      ARRAY[gid] AS idlist
    FROM nyc_subway_stations
    WHERE gid = 304)
    UNION ALL
    (SELECT
      s.geom,
      array_append(n.idlist, s.gid) AS idlist
    FROM nyc_subway_stations s, next_stop n
    WHERE strpos(s.routes, 'Q') != 0
    AND NOT n.idlist @> ARRAY[s.gid]
    ORDER BY ST_Distance(n.geom, s.geom) ASC
    LIMIT 1)
)
SELECT ST_MakeLine(geom) AS geom FROM next_stop;

Det ser ut så här:

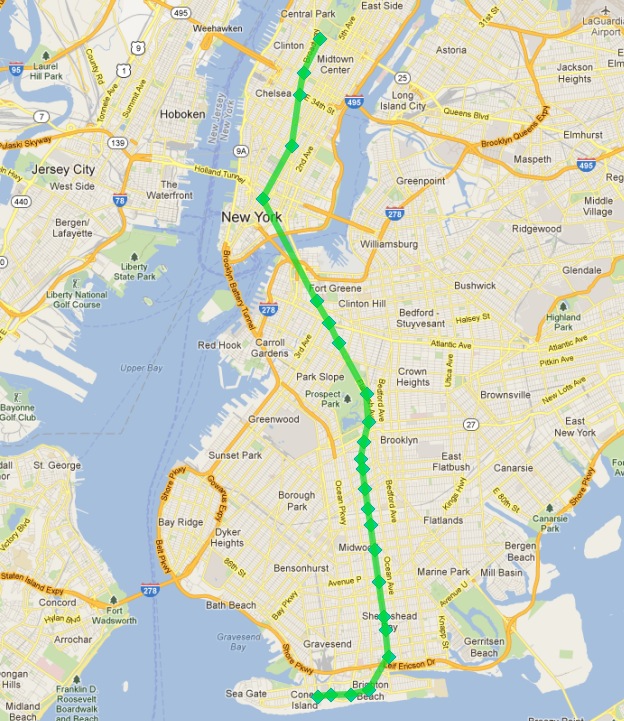
Lyckades!

Men det finns två problem:

Vi beräknar bara en tunnelbanelinje här, men vi vill beräkna alla linjer.
Vår fråga innehåller en del apriori-kunskap, den första stationsidentifieraren som fungerar som frö för den sökalgoritm som bygger rutten.

Låt oss ta itu med det svåra problemet först, att räkna ut den första stationen på en rutt utan att manuellt titta på de stationer som ingår i rutten.

Våra Q-tågstopp kan fungera som en utgångspunkt. Vad kännetecknar slutstationerna på rutten?

Ett svar är ”det är de nordligaste och sydligaste stationerna”. Men tänk om Q-tåget gick från öst till väst. Skulle villkoret fortfarande gälla?

En mindre riktad karaktärisering av ändstationerna är ”de är de stationer som ligger längst bort från mitten av rutten”. Med denna karaktärisering spelar det ingen roll om linjen går i nord-sydlig eller öst-västlig riktning, bara den går i mer eller mindre en riktning, särskilt i ändarna.

Eftersom det inte finns någon 100% heuristik för att räkna ut slutpunkterna, låt oss prova denna andra regel.

Observera

Ett uppenbart fel på regeln ”längst bort från mitten” är en cirkulär linje, som Circle Line i London, Storbritannien. Lyckligtvis finns det inga sådana linjer i New York!

För att räkna ut slutstationerna för varje rutt måste vi först ta reda på vilka rutter det finns! Vi hittar de olika rutterna.

WITH routes AS (
  SELECT DISTINCT unnest(string_to_array(routes,',')) AS route
  FROM nyc_subway_stations ORDER BY route
)
SELECT * FROM routes;

Observera användningen av två avancerade PostgreSQL ARRAY-funktioner:

string_to_array tar in en sträng och delar upp den i en matris med hjälp av ett separatortecken. PostgreSQL stöder matriser av vilken typ som helst, så det är möjligt att bygga matriser av strängar, som i det här fallet, men också av geometrier och geografier som vi kommer att se senare i detta exempel.
unnest tar in en matris och bygger en ny rad för varje post i matrisen. Effekten är att en ”horisontell” matris som är inbäddad i en enda rad omvandlas till en ”vertikal” matris med en rad för varje värde.

Resultatet är en lista över alla unika identifikatorer för tunnelbanelinjer.

 route
-------
 1
 2
 3
 4
 5
 6
 7
 A
 B
 C
 D
 E
 F
 G
 J
 L
 M
 N
 Q
 R
 S
 V
 W
 Z
(24 rows)

Vi kan bygga vidare på detta resultat genom att koppla det till tabellen nyc_subway_stations för att skapa en ny tabell som för varje rutt innehåller en rad för varje station på rutten.

WITH routes AS (
  SELECT DISTINCT unnest(string_to_array(routes,',')) AS route
  FROM nyc_subway_stations ORDER BY route
),
stops AS (
  SELECT s.gid, s.geom, r.route
  FROM routes r
  JOIN nyc_subway_stations s
  ON (strpos(s.routes, r.route) <> 0)
)
SELECT * FROM stops;

 gid |                      geom                      | route
-----+----------------------------------------------------+-------
   2 | 010100002026690000CBE327F938CD21415EDBE1572D315141 | 1
   3 | 010100002026690000C676635D10CD2141A0ECDB6975305141 | 1
  20 | 010100002026690000AE59A3F82C132241D835BA14D1435141 | 1
  22 | 0101000020266900003495A303D615224116DA56527D445141 | 1
                            ...etc...

Nu kan vi hitta mittpunkten genom att samla alla stationer för varje rutt i en enda multipunkt och beräkna centroiden för den multipunkten.

WITH routes AS (
  SELECT DISTINCT unnest(string_to_array(routes,',')) AS route
  FROM nyc_subway_stations ORDER BY route
),
stops AS (
  SELECT s.gid, s.geom, r.route
  FROM routes r
  JOIN nyc_subway_stations s
  ON (strpos(s.routes, r.route) <> 0)
),
centers AS (
  SELECT ST_Centroid(ST_Collect(geom)) AS geom, route
  FROM stops
  GROUP BY route
)
SELECT * FROM centers;

Mittpunkten för samlingen av ”Q”-tågstopp ser ut så här:

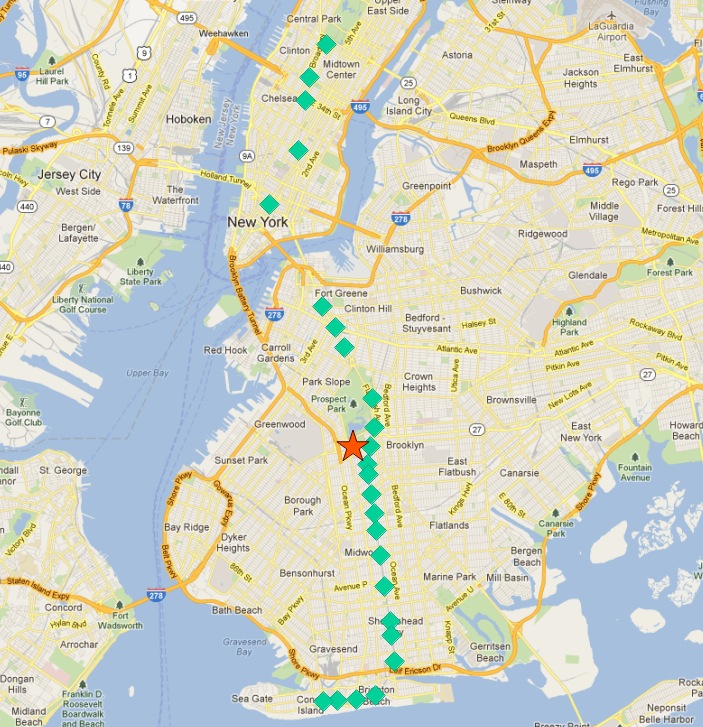
Så den nordligaste hållplatsen, slutpunkten, verkar också vara den hållplats som ligger längst bort från centrum. Låt oss beräkna den längsta punkten för varje rutt.

WITH routes AS (
  SELECT DISTINCT unnest(string_to_array(routes,',')) AS route
  FROM nyc_subway_stations ORDER BY route
),
stops AS (
  SELECT s.gid, s.geom, r.route
  FROM routes r
  JOIN nyc_subway_stations s
  ON (strpos(s.routes, r.route) <> 0)
),
centers AS (
  SELECT ST_Centroid(ST_Collect(geom)) AS geom, route
  FROM stops
  GROUP BY route
),
stops_distance AS (
  SELECT s.*, ST_Distance(s.geom, c.geom) AS distance
  FROM stops s JOIN centers c
  ON (s.route = c.route)
  ORDER BY route, distance DESC
),
first_stops AS (
  SELECT DISTINCT ON (route) stops_distance.*
  FROM stops_distance
)
SELECT * FROM first_stops;

Vi har lagt till två underfrågor den här gången:

stops_distance kopplar ihop centrumpunkterna med stationstabellen och beräknar avståndet mellan stationerna och centrum för varje rutt. Resultatet ordnas så att posterna kommer ut i satser för varje rutt, med den station som ligger längst bort som första post i satsen.
first_stops filtrerar stops_distance-utdata genom att endast ta den första posten för varje distinkt grupp. På grund av hur vi beställde stops_distance är den första posten den längsta posten, vilket innebär att det är den station vi vill använda som startpunkt för att bygga varje tunnelbanesträcka.

Nu känner vi till varje rutt och vi vet (ungefär) vilken station varje rutt startar från: vi är redo att generera ruttlinjerna!

Men först måste vi omvandla vårt rekursiva CTE-uttryck till en funktion som vi kan anropa med parametrar.

CREATE OR REPLACE function walk_subway(integer, text) returns geometry AS
$$
WITH RECURSIVE next_stop(geom, idlist) AS (
    (SELECT
      geom AS geom,
      ARRAY[gid] AS idlist
    FROM nyc_subway_stations
    WHERE gid = $1)
    UNION ALL
    (SELECT
      s.geom AS geom,
      array_append(n.idlist, s.gid) AS idlist
    FROM nyc_subway_stations s, next_stop n
    WHERE strpos(s.routes, $2) != 0
    AND NOT n.idlist @> ARRAY[s.gid]
    ORDER BY ST_Distance(n.geom, s.geom) ASC
    LIMIT 1)
)
SELECT ST_MakeLine(geom) AS geom
FROM next_stop;
$$
language 'sql';

Och nu är vi redo att åka!

CREATE TABLE nyc_subway_lines AS
-- Distinct route identifiers!
WITH routes AS (
  SELECT DISTINCT unnest(string_to_array(routes,',')) AS route
  FROM nyc_subway_stations ORDER BY route
),
-- Joined back to stops! Every route has all its stops!
stops AS (
  SELECT s.gid, s.geom, r.route
  FROM routes r
  JOIN nyc_subway_stations s
  ON (strpos(s.routes, r.route) <> 0)
),
-- Collects stops by routes and calculate centroid!
centers AS (
  SELECT ST_Centroid(ST_Collect(geom)) AS geom, route
  FROM stops
  GROUP BY route
),
-- Calculate stop/center distance for each stop in each route.
stops_distance AS (
  SELECT s.*, ST_Distance(s.geom, c.geom) AS distance
  FROM stops s JOIN centers c
  ON (s.route = c.route)
  ORDER BY route, distance DESC
),
-- Filter out just the furthest stop/center pairs.
first_stops AS (
  SELECT DISTINCT ON (route) stops_distance.*
  FROM stops_distance
)
-- Pass the route/stop information into the linear route generation function!
SELECT
  ascii(route) AS gid, -- QGIS likes numeric primary keys
  route,
  walk_subway(gid, route) AS geom
FROM first_stops;

-- Do some housekeeping too
ALTER TABLE nyc_subway_lines ADD PRIMARY KEY (gid);

Så här ser vår slutliga tabell ut visualiserad i QGIS:

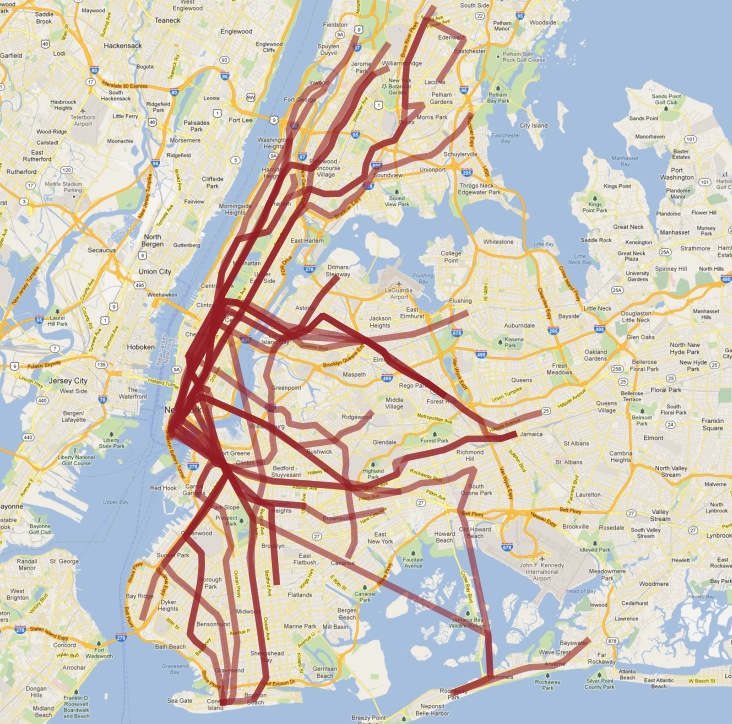
Som vanligt finns det vissa problem med vår enkla förståelse av uppgifterna:

det finns faktiskt två S-tåg (short distance ”shuttle”), ett på Manhattan och ett i Rockaways, och vi slår ihop dem eftersom de båda heter S;
4-tåget (och några andra) delar sig i slutet av en linje till två ändstationer, så antagandet ”följ en linje” bryts och resultatet har en rolig krok i slutet.

Förhoppningsvis har detta exempel gett en smak av några av de komplexa datamanipulationerna som är möjliga genom att kombinera de avancerade funktionerna i PostgreSQL och PostGIS.

Introduction to PostGIS

40. Avancerade geometriska konstruktioner¶

40.1. Se även¶

Introduction to PostGIS

40. Avancerade geometriska konstruktioner¶

40.1. Se även¶

Navigation