24. Jämlikhet

24.1. Jämlikhet

Det kan vara knepigt att bestämma jämlikhet när man hanterar geometrier. PostGIS stöder tre olika funktioner som kan användas för att bestämma olika nivåer av jämlikhet, men för tydlighetens skull använder vi definitionerna nedan. För att illustrera dessa funktioner kommer vi att använda följande polygoner.

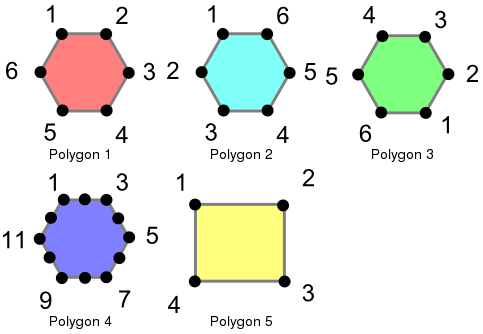
Dessa polygoner laddas med hjälp av följande kommandon.

CREATE TABLE polygons (id integer, name varchar, poly geometry);

INSERT INTO polygons VALUES
  (1, 'Polygon 1', 'POLYGON((-1 1.732,1 1.732,2 0,1 -1.732,
      -1 -1.732,-2 0,-1 1.732))'),
  (2, 'Polygon 2', 'POLYGON((-1 1.732,-2 0,-1 -1.732,1 -1.732,
      2 0,1 1.732,-1 1.732))'),
  (3, 'Polygon 3', 'POLYGON((1 -1.732,2 0,1 1.732,-1 1.732,
      -2 0,-1 -1.732,1 -1.732))'),
  (4, 'Polygon 4', 'POLYGON((-1 1.732,0 1.732, 1 1.732,1.5 0.866,
      2 0,1.5 -0.866,1 -1.732,0 -1.732,-1 -1.732,-1.5 -0.866,
      -2 0,-1.5 0.866,-1 1.732))'),
  (5, 'Polygon 5', 'POLYGON((-2 -1.732,2 -1.732,2 1.732,
      -2 1.732,-2 -1.732))');

24.1.1. Exakt lika

Exakt likhet bestäms genom att jämföra två geometrier, toppunkt för toppunkt, i ordning för att säkerställa att de är identiska i position. Följande exempel visar hur denna metod kan vara begränsad i sin effektivitet.

SELECT a.name, b.name,
  CASE WHEN ST_OrderingEquals(a.poly, b.poly)
       THEN 'Exactly Equal'
       ELSE 'Not Exactly Equal' END
  FROM polygons AS a, polygons AS b;

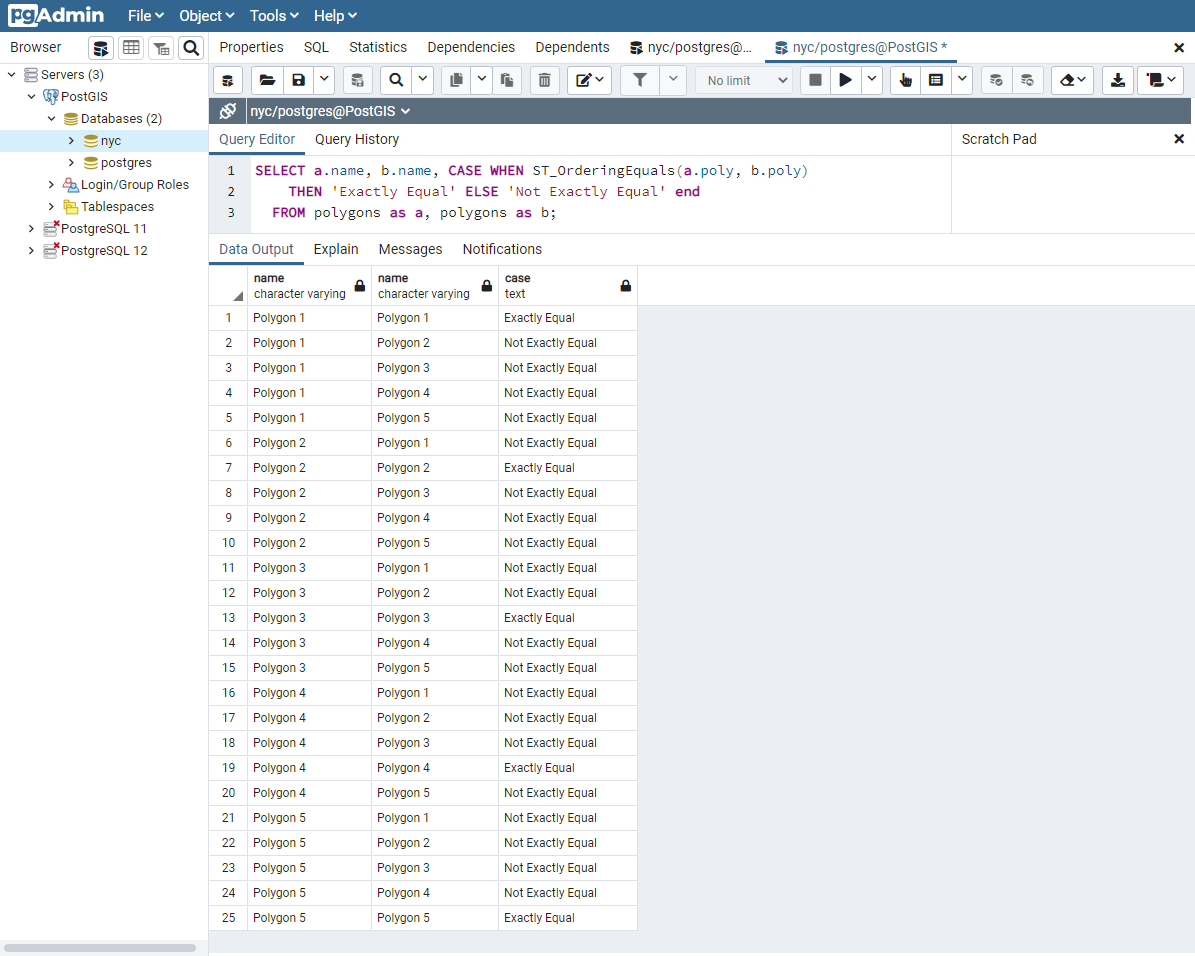
I det här exemplet är polygonerna bara lika med sig själva, inte med andra till synes likvärdiga polygoner (som i fallet med polygonerna 1 till 3). I fallet med polygonerna 1, 2 och 3 är hörnen identiskt placerade men definierade i olika ordning. Polygon 4 har kolinjära (och därmed överflödiga) hörn på hexagonkanterna, vilket orsakar ojämlikhet med polygon 1.

24.1.2. Spatialt lika

Som vi såg ovan tar exakt likhet inte hänsyn till geometriernas spatiala karaktär. Det finns en funktion, med det passande namnet ST_Equals, för att testa geometriers spatiala jämlikhet eller ekvivalens.

SELECT a.name, b.name,
  CASE WHEN ST_Equals(a.poly, b.poly)
       THEN 'Spatially Equal'
       ELSE 'Not Equal' END
  FROM polygons AS a, polygons AS b;

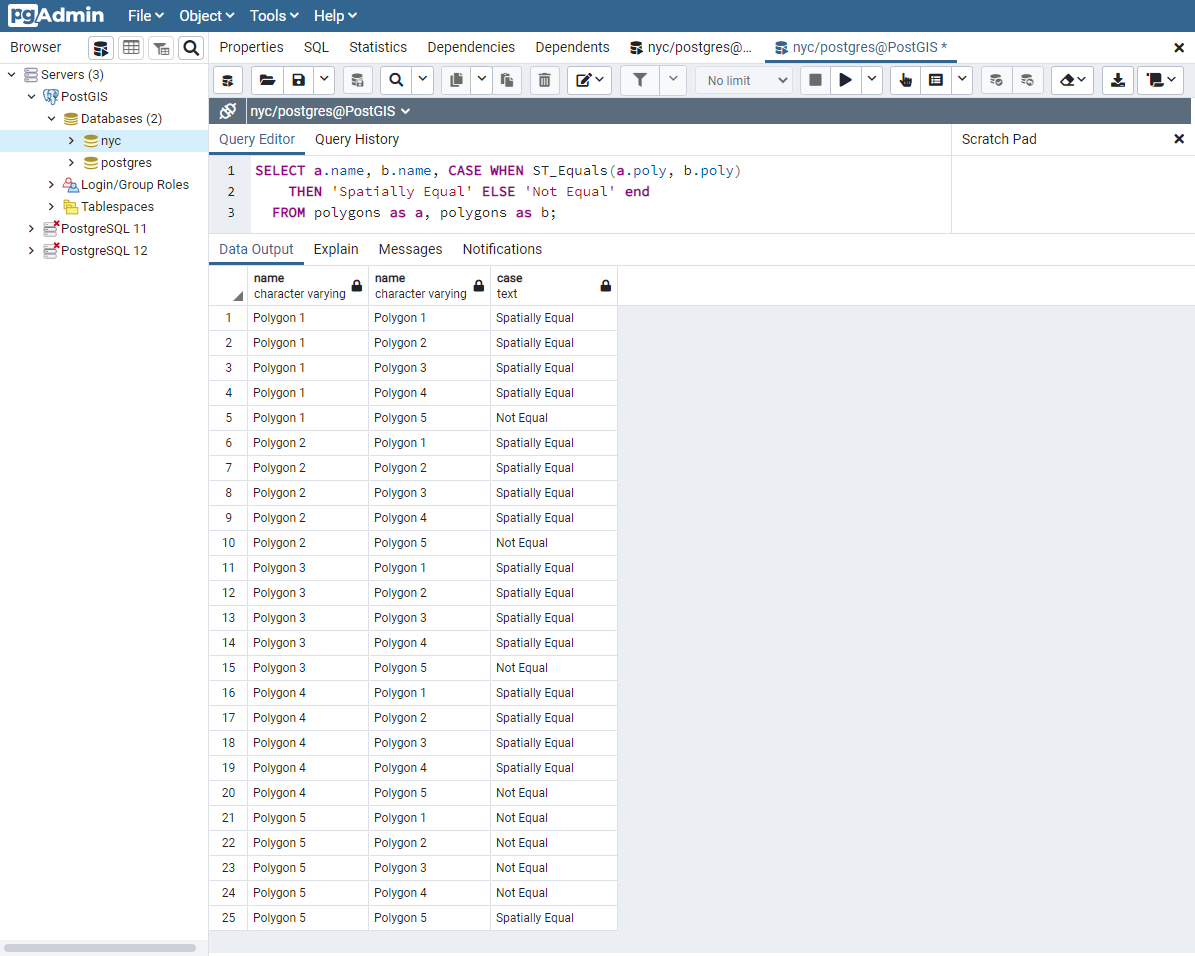
Dessa resultat är mer i linje med vår intuitiva förståelse av jämlikhet. Polygonerna 1 till 4 anses vara lika, eftersom de omsluter samma område. Observera att varken polygonens riktning, startpunkten för polygonens definition eller antalet punkter som används är viktiga här. Det viktiga är att polygonerna innehåller samma utrymme.

24.1.3. Jämna gränser

Exakt likhet kräver, i värsta fall, jämförelse av varje enskilt vertex i geometrin för att fastställa likhet. Detta kan ta lång tid och är kanske inte lämpligt för att jämföra ett stort antal geometrier. För att möjliggöra snabbare jämförelser finns operatorn equal bounds, ~=. Denna operatör verkar endast på den avgränsande rutan (rektangeln) och säkerställer att geometrierna har samma tvådimensionella utsträckning, men inte nödvändigtvis samma utrymme.

SELECT a.name, b.name,
  CASE WHEN a.poly ~= b.poly
       THEN 'Equal Bounds'
       ELSE 'Non-equal Bounds' END
  FROM polygons AS a, polygons AS b;

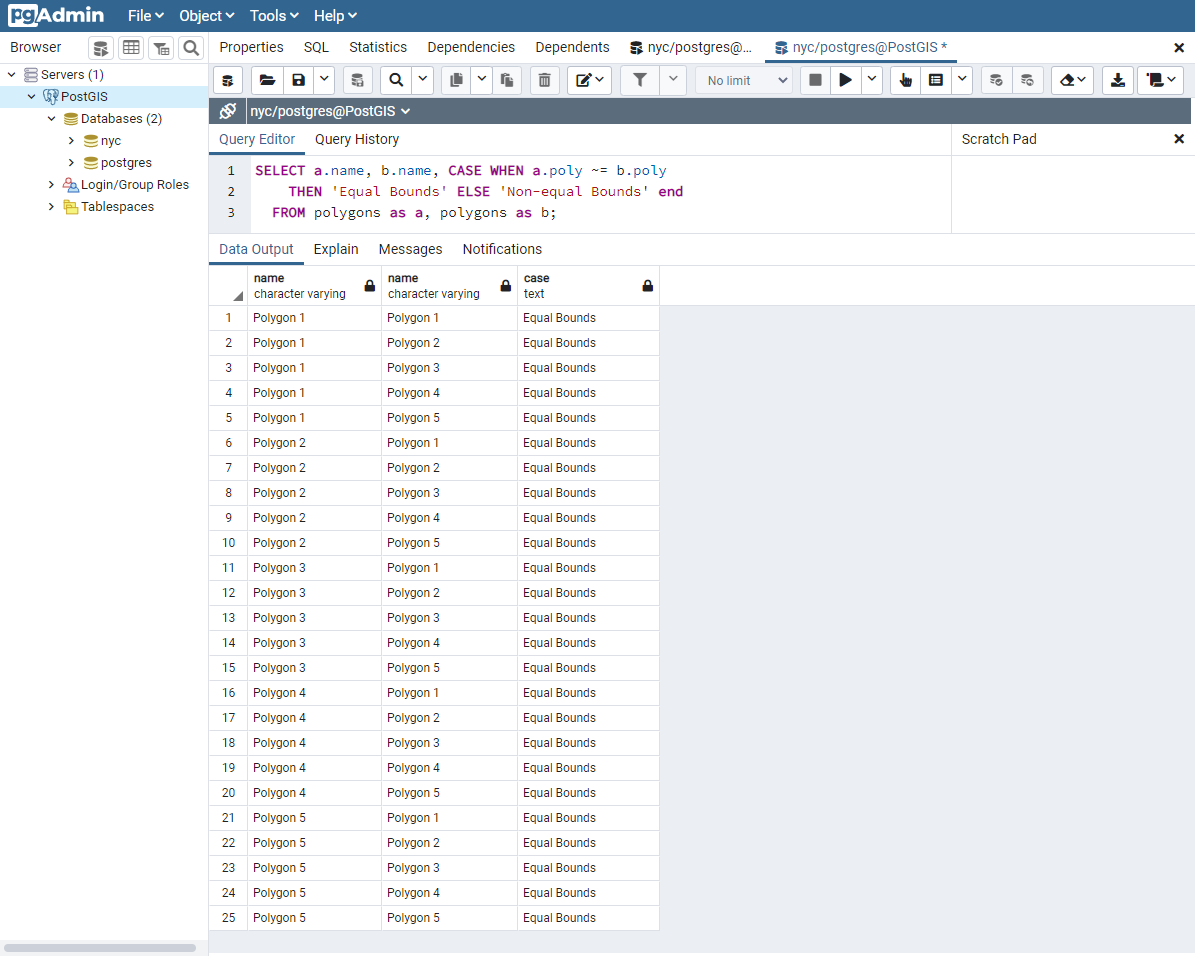
Som du kan se har alla våra spatialt lika geometrier också lika gränser. Tyvärr returneras Polygon 5 också som lika i det här testet, eftersom den delar samma bounding box som de andra geometrierna. Varför är då detta användbart? Även om detta kommer att behandlas i detalj senare är det korta svaret att detta möjliggör användning av spatial indexering som snabbt kan reducera enorma jämförelseuppsättningar till mer hanterbara block när data sammanfogas eller filtreras.