32. Grundläggande topologityper

Innan du läser detta dokument ska du åtminstone titta på ett av dessa dokument:

Introduktiv workshop: PostGIS Topology Workshop.

Handbok: PostGIS-topologi.

ISO Topology: OGC-SFS Geometries.

I den här workshopen kommer vi att gå igenom några grundläggande principer för topologi, dess grunder och definitioner. Det är inte tänkt att vara ett sätt att använda dem direkt, utan att förstå det för att sedan kunna använda det enkelt.

32.1. Types

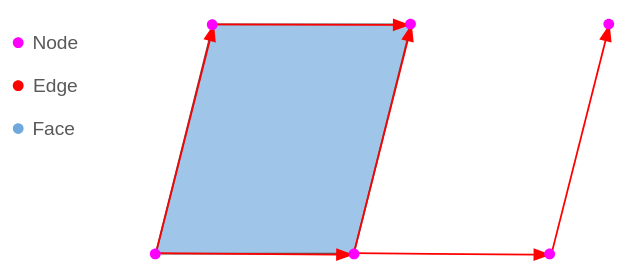
Den grundläggande topologin fungerar på tre grundläggande typer.

• Node: 2D-punkt, allt börjar eller slutar här

• Edge: En linestring med riktning som börjar och slutar på en nod

• Face: Sluten uppsättning linestrings, som anpassar sig till en polygon

Det finns vissa regler för att en uppsättning noder, kanter och ytor ska vara giltiga, se ISO Topology-dokumentet, som har en mycket bra sammanfattning av dessa villkor, en topologi som följer alla regler är en giltig topologi.

Det är bra att veta, fram till nu sparar Postgis all denna information internt, varje typ har sitt eget unika ID, och med det kan vi redigera och ändra dem med hjälp av tillgängliga funktioner, till exempel med ST_RemEdgeNewFace kan du ta bort en kant och skapa en ny yta.

Men det finns fortfarande en sak som saknas, hur säger vi till exempel att ett ansikte har ett specifikt attribut? Postgis implementerar flera koncept för att göra detta som Layers, TopoGeometry, TopoElement.

32.2. Universal Face

Det kan vara intuitivt att tro att bara de faces som konstrueras av kanter existerar, men det finns ett undantag: allt vitt utrymme bland alla faces är också ett face!

Det tomma utrymmet kallas Universal Face, när en topologi är tom är allt utrymme Universal Face, när vi lägger till en linestring är en kant av detta ansikte, när vi sedan gör en polygon är det som att göra ett hål i ansiktet och stjäla det för att tilldela det till ett ansikte.

Denna yta är oändlig och har inte någon gräns.

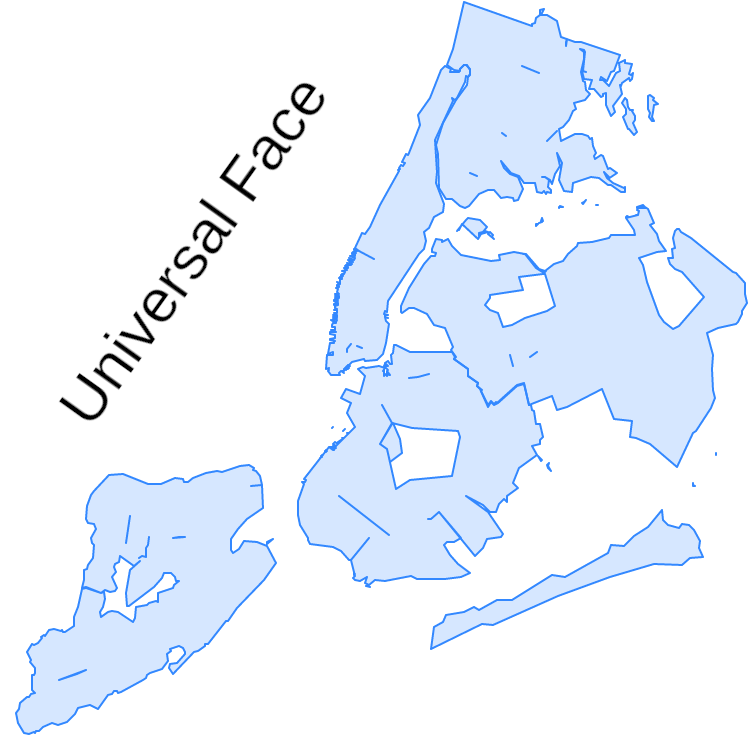
Universal Face har ID 0.

32.3. Tolkning av kanter

För att korrekt representera en topologi och dess former finns det vissa definitioner som används för att konstruera de tabeller som lagrar allt, kanten är på de mer komplexa.

All information om kanter lagras i tabellen edge_data, i ditt anpassade topologischema, och vilken information behöver vi i kanterna? i princip är det information om noder och ansikten, kanten är den primitiva som förbinder båda.

Dessa linestrings kallas Edges eftersom de är kanterna på ytorna.

32.3.1. Kantriktning, vänster och höger

Kanter i topologin har ett rätt definierat perspektiv och vy, när vi ser dem måste det göras på nästa sätt:

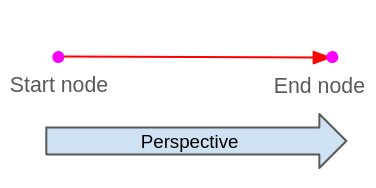
När vi vill se från kantperspektivet är det alltid från slutnoden till startkanten, alltid med kanten framåt.

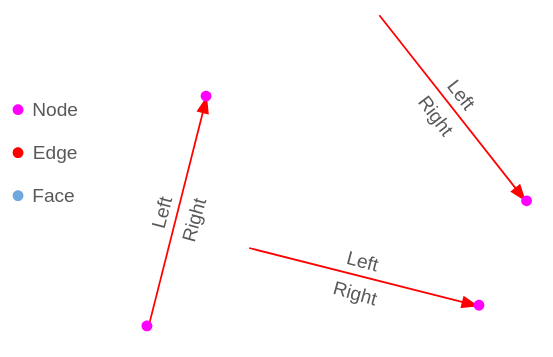
Kanterna har vänster- och högeregenskaper, som vi ser definieras de med hjälp av kantperspektivet, se linjesträngen från startnoden till slutnoden, det kommer alltid att finnas en väldefinierad vänster och höger.

Så se kanten framåt och du har alltid en vänster och en höger sida.

Detta hjälper till att relatera vilka ytor som finns på vardera sidan av kanten:

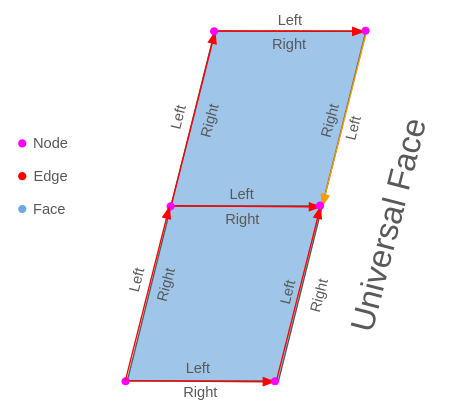
Kontrollera kanterna på bilden, medan nästan alla kanter går från ner till upp och från vänster till höger, finns det en orange kant som har motsatt riktning, så dess sidor vänster och höger är ombytta i förhållande till de andra, men om du tittar på kanten framåt är höger och vänster rätt.

Fortsätt att se den orange kanten, medan den till höger har en polygon byggd av kanterna, till vänster är Universal Face.

När vi vill analysera en kant, och vi måste se den från kantperspektivet, är det alltid att titta på kanten framåt, aldrig bakåt!

Vilka är alla de kommande kanterna? Om vi tittar framåt går vi från startnoden till slutnoden, alla kanter som börjar eller slutar i kantnoden!

32.4. Kantdata

Tabellen edge_data innehåller information om kanten, utifrån vad vi vet just nu kan vi tolka nästa kolumner:

• edge_id: Unikt ID för kanten

• start_node: ID för den nod som är densamma som startpunkten för kanten

• end_node: ID för den nod som är densamma som slutpunkten för kanten

• left_face: ID för ytan till vänster om kanten

• right_face: ID för ytan till höger om kanten

• geom: Geometri för kanten

32.4.1. Abs Next Edge & Next Edge

Tabellen edge_data har kolumnerna abs_next_left_edge och abs_next_right_edge, och nu blir det lite knepigt att tolka dem.

Hittills har vi främst sett egenskaper hos själva kanten och vad som har på sidorna, nästa kants egenskaper är annorlunda, fråga inte bara om själva kanten, det handlar om vilken som är nästa kant som bygger ansiktet till höger eller vänster.

Logiken för höger_kant och vänster_kant är mycket lika, så vi kommer först att titta på den vänstra djupare och sedan visa den högra.

Vi kommer att använda nästa topologi som exempel:

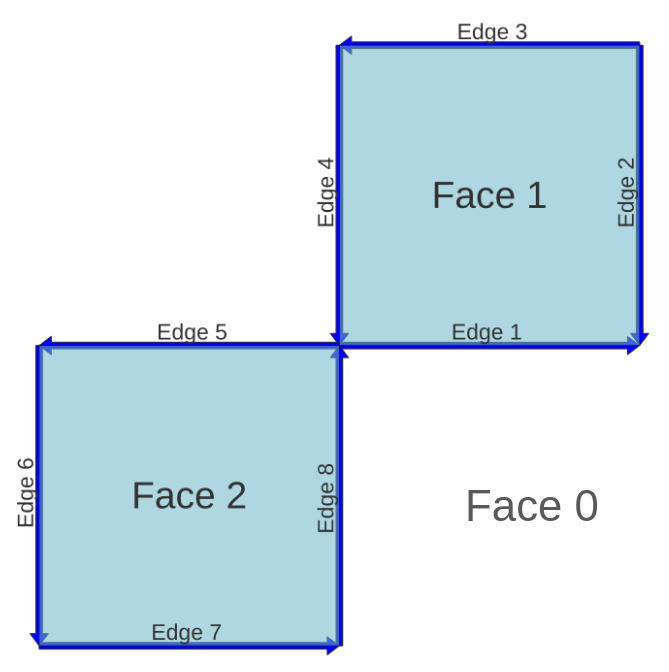
32.4.1.1. Vänster

Låt oss ta Edge 5 som exempel, den här har till vänster Face 2, om vi tittar framåt vilken är nästa edge vem bygger Face 2?

Det här är Edge 6.

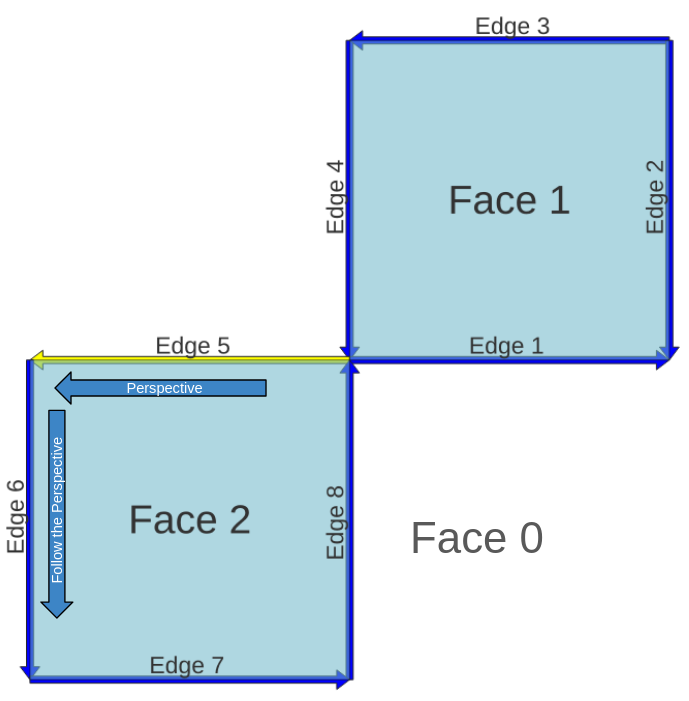
Något mycket viktigt här är perspektivet vi följer linjerna, beroende på kantriktningen, är det som att se detta face medurs eller moturs.

Med denna information har vi abs_next_left_edge som kommer att vara 6.

next_left_edge är nästan samma sak som abs_next_left_edge, förutom att den kan vara negativ, vilket beror på vilket perspektiv vi ser kanten från.

Om vi följer Edge-perspektivet kommer vi att ha två riktningar, riktningen mot nästa kant och riktningen för perspektivet på nästa kant.

Vi kommer att använda nästa tecken i varje fall:

• Perspektivriktning och riktning mot nästa kant är motsatta: ”-”

• Perspektivriktningen och Next edge-riktningen är desamma: None, behåll värdet positivt

Eftersom perspektivet och Edge 6 har samma riktning kommer next_left_edge att vara 6.

• abs_next_left_edge: 6

• next_left_edge: 6

32.4.1.2. Höger

Den enda skillnaden mellan vänster och höger analys är perspektivet, medan vi i vänster använder framåt, kommer vi i höger att se bakåt. Var försiktig, även om vi tittar bakåt är definitionen av Left Face och Right Face fortfarande densamma, framåtblickande! Det är bara perspektivet som ändras.

Edge 5 har Face 0 på sin högra sida, Universal Face, om man tittar Edge 5 bakåt är nästa kant som bygger Face 0 Edge 4.

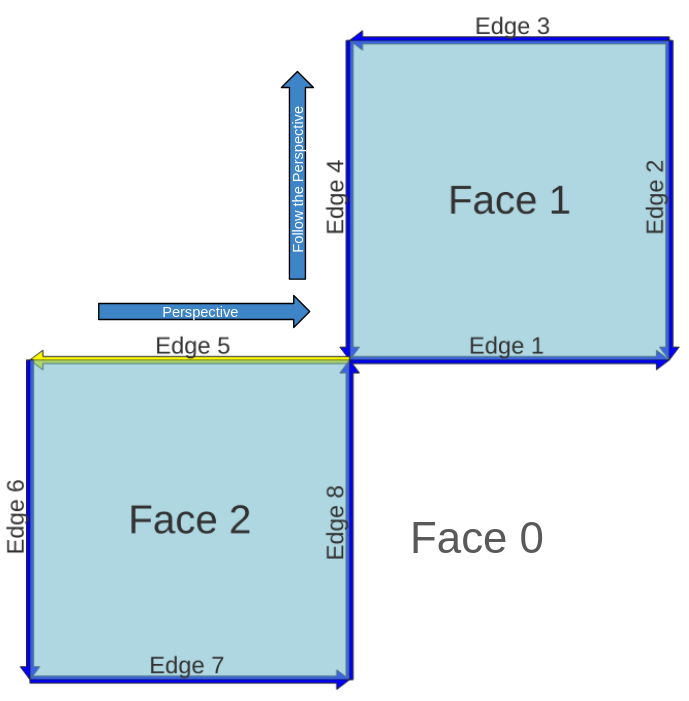
Om vi följer perspektivet för Edge 5 på Edge 4 kan vi se att den går upp, medan Edge 4 går ner, perspektivets riktning och Edge 4:s riktning är motsatta.

• abs_next_right_edge: 4

• nexr_right_edge: -4 (Perspektivriktning och Edge 4-riktning är motsatta)

32.4.1.3. Isolerat kantfall

Det finns ett fall som kan vara förvirrande, alla regler ovan följer på samma sätt men det är bra att ta en titt.

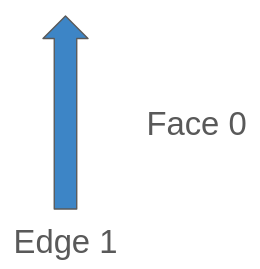
När vi har en kant som inte har några kopplingar till andra kanter är det första vi kan förstå att vänstersidan är densamma som högersidan, i det här fallet Face 0, Universal Face.

Om vi följer den tidigare logiken, till vänster är Face 0, vilket är nästa kant som bygger Face 0? Det finns faktiskt en kant, och den är sig själv, och den har också ett perspektiv som tidigare:

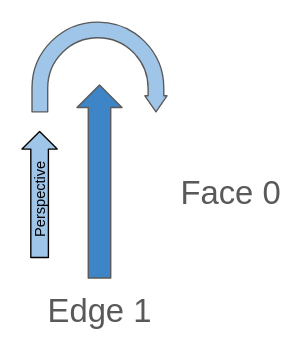
Om vi kontrollerar perspektivriktningen slutar vi titta på samma kant men i motsatt riktning, vilket innebär att Edge 1 och dess nästa kant (Edge 1) har motsatta riktningar.

• edge_id: 1

• abs_next_left_edge: 1

• next_left_edge: -1 (Detta kommer alltid att vara negativt när vi ser framåt en isolerad kant)

För nästa högra kant är densamma, nästa kant kommer att vara sig själv, det enda som förändras är perspektivet:

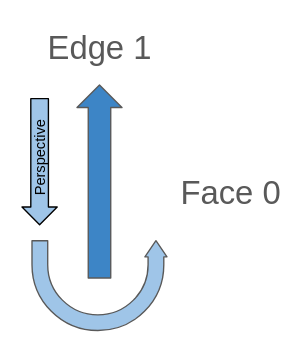
När vi tittar bakåt på en isolerad kant kommer perspektivet alltid att ha samma riktning som kanten:

• edge_id: 1

• abs_next_right_edge: 1

• next_right_edge: -1 (Detta kommer alltid att vara positivt medan vi ser bakåt en isolerad kant)

32.4.2. Fullständiga kolumner av edge_data

Vi har redan kontrollerat alla kolumner i tabellen edge_data:

• edge_id: Unikt ID för kanten.

• start_node: ID för den nod som är densamma som startpunkten för kanten.

• end_node: ID för den nod som är densamma som slutpunkten för kanten.

• left_face: ID för den yta som ligger till vänster om kanten.

• abs_next_left_edge: Nästa kant som bygger ansiktet till vänster.

• next_left_edge: abs_next_left_edge och negativt tecken om den högra sidan är till höger om nästa vänstra kant.

• right_face: ID för ytan till höger om kanten.

• abs_next_right_edge: Nästa kant som bygger ansiktet till höger.

• next_right_edge: abs_next_right_edge och negativt tecken om den vänstra sidan är till höger om nästa högra kant.

• geom: Geometri för kanten.