statistics — Matematiska statistikfunktioner

Tillagd i version 3.4.

Källkod: Lib/statistics.py

---

Denna modul innehåller funktioner för att beräkna matematisk statistik för numeriska (Real-värderade) data.

Modulen är inte avsedd att vara en konkurrent till tredjepartsbibliotek som NumPy, SciPy, eller egenutvecklade statistikpaket med fullständiga funktioner som riktar sig till professionella statistiker som Minitab, SAS och Matlab. Programmet är anpassat för grafräknare och vetenskapliga räknare.

Om inte annat uttryckligen anges, stöder dessa funktioner int, float, Decimal och Fraction. Beteende med andra typer (oavsett om de finns i det numeriska tornet eller inte) stöds för närvarande inte. Samlingar med en blandning av typer är också odefinierade och beroende av implementering. Om dina indata består av blandade typer kan du kanske använda map() för att säkerställa ett konsekvent resultat, till exempel: map(float, input_data).

I vissa dataset används NaN-värden (not a number) för att representera saknade data. Eftersom NaN-värden har en ovanlig jämförelsesemantik orsakar de överraskande eller odefinierade beteenden i statistikfunktioner som sorterar data eller räknar förekomster. De funktioner som påverkas är median(), median_low(), median_high(), median_grouped(), mode(), multimode() och quantiles(). NaN-värdena bör tas bort innan du anropar dessa funktioner:

>>> from statistics import median
>>> from math import isnan
>>> from itertools import filterfalse

>>> data = [20.7, float('NaN'),19.2, 18.3, float('NaN'), 14.4]
>>> sorted(data)  # This has surprising behavior
[20.7, nan, 14.4, 18.3, 19.2, nan]
>>> median(data)  # This result is unexpected
16.35

>>> sum(map(isnan, data))    # Number of missing values
2
>>> clean = list(filterfalse(isnan, data))  # Strip NaN values
>>> clean
[20.7, 19.2, 18.3, 14.4]
>>> sorted(clean)  # Sorting now works as expected
[14.4, 18.3, 19.2, 20.7]
>>> median(clean)       # This result is now well defined
18.75

Medelvärden och mått på centralt läge

Dessa funktioner beräknar ett genomsnittligt eller typiskt värde från en population eller ett urval.

medelvärde()	Aritmetiskt medelvärde (”average”) av data.
fmean()	Snabbt aritmetiskt medelvärde med flyttal, med valfri viktning.
geometric_mean()	Geometriskt medelvärde av data.
harmonic_mean()	Harmoniskt medelvärde av data.
kde()	Uppskatta sannolikhetstäthetsfördelningen för data.
kde_random()	Slumpmässigt urval från den PDF som genereras av kde().
median()	Median (medelvärde) av data.
median_low()	Låg median av data.
median_high()	Hög median av data.
median_grouped()	Median (50:e percentilen) för grupperade data.
mode()	Single mode (vanligaste värdet) av diskreta eller nominella data.
multimode()	Lista över lägen (de vanligaste värdena) för diskreta eller nominella data.
quantiles()	Dela in data i intervall med lika stor sannolikhet.

Mått på spridning

Dessa funktioner beräknar ett mått på hur mycket populationen eller urvalet tenderar att avvika från de typiska eller genomsnittliga värdena.

pstdev()	Standardavvikelse för data i populationen.
pvariance()	Populationsvarians för data.
stdev()	Standardavvikelse för data.
variance()	Provvarians av data.

Statistik för relationer mellan två inmatningar

Dessa funktioner beräknar statistik avseende relationer mellan två indata.

covariance()	Provkovarians för två variabler.
correlation()	Pearson och Spearmans korrelationskoefficienter.
linear_regression()	Lutning och intercept för enkel linjär regression.

Funktionsdetaljer

Observera: Funktionerna kräver inte att de data som ges till dem är sorterade. För att underlätta läsningen visas dock sorterade sekvenser i de flesta exemplen.

statistics.mean(data)

Returnerar det aritmetiska medelvärdet för data som kan vara en sekvens eller iterabel.

Det aritmetiska medelvärdet är summan av data dividerat med antalet datapunkter. Det kallas ofta för ”genomsnittet”, även om det bara är ett av många olika matematiska genomsnitt. Det är ett mått på den centrala placeringen av data.

Om data är tom, kommer StatisticsError att uppstå.

Några exempel på användning:

>>> mean([1, 2, 3, 4, 4])
2.8
>>> mean([-1.0, 2.5, 3.25, 5.75])
2.625

>>> from fractions import Fraction as F
>>> mean([F(3, 7), F(1, 21), F(5, 3), F(1, 3)])
Fraction(13, 21)

>>> from decimal import Decimal as D
>>> mean([D("0.5"), D("0.75"), D("0.625"), D("0.375")])
Decimal('0.5625')

Anteckning

Medelvärdet påverkas starkt av extremvärden och är inte nödvändigtvis ett typiskt exempel på datapunkterna. För ett mer robust, men mindre effektivt, mått på central tendens, se median().

Medelvärdet för urvalet ger en opartisk uppskattning av det sanna populationsmedelvärdet, så att när det tas som ett genomsnitt över alla möjliga urval, konvergerar mean(sample) mot det sanna medelvärdet för hela populationen. Om data representerar hela populationen snarare än ett urval, är mean(data) likvärdigt med att beräkna det sanna populationsmedelvärdet μ.

statistics.fmean(data, weights=None)

Konvertera data till flyttal och beräkna det aritmetiska medelvärdet.

Detta går snabbare än funktionen mean() och returnerar alltid en float. Data kan vara en sekvens eller iterabel. Om indatauppsättningen är tom, returneras ett StatisticsError.

>>> fmean([3.5, 4.0, 5.25])
4.25

Valfri viktning stöds. En professor kan till exempel sätta betyg på en kurs genom att vikta frågesporter med 20 %, hemuppgifter med 20 %, en halvtidstentamen med 30 % och en sluttentamen med 30 %:

>>> grades = [85, 92, 83, 91]
>>> weights = [0.20, 0.20, 0.30, 0.30]
>>> fmean(grades, weights)
87.6

Om weights anges måste den vara lika lång som data, annars uppstår ett ValueError.

Tillagd i version 3.8.

Ändrad i version 3.11: Lagt till stöd för vikter.

statistics.geometric_mean(data)

Konvertera data till flyttal och beräkna det geometriska medelvärdet.

Det geometriska medelvärdet anger den centrala tendensen eller det typiska värdet för data genom att använda produkten av värdena (i motsats till det aritmetiska medelvärdet som använder summan av värdena).

Utlöser ett StatisticsError om indatadatasetet är tomt, om det innehåller en nolla eller om det innehåller ett negativt värde. Data kan vara en sekvens eller iterabel.

Inga särskilda ansträngningar görs för att uppnå exakta resultat. (Detta kan dock komma att ändras i framtiden.)

>>> round(geometric_mean([54, 24, 36]), 1)
36.0

Tillagd i version 3.8.

statistics.harmonic_mean(data, weights=None)

Returnerar det harmoniska medelvärdet av data, en sekvens eller iterabel av realvärdesberäknade tal. Om weights utelämnas eller None, antas lika viktning.

Det harmoniska medelvärdet är reciprokvärdet av det aritmetiska mean() av de reciproka värdena i data. Till exempel kommer det harmoniska medelvärdet av tre värden a, b och c att motsvara 3/(1/a + 1/b + 1/c). Om ett av värdena är noll blir resultatet noll.

Det harmoniska medelvärdet är en typ av medelvärde, ett mått på den centrala platsen för data. Det är ofta lämpligt vid medelvärdesberäkning av förhållanden eller hastigheter, t.ex. hastigheter.

Antag att en bil färdas 10 km i 40 km/tim och sedan ytterligare 10 km i 60 km/tim. Vad är medelhastigheten?

>>> harmonic_mean([40, 60])
48.0

Antag att en bil kör 40 km/tim i 5 km och när trafiken släpper ökar hastigheten till 60 km/tim under de återstående 30 km av färden. Vad är den genomsnittliga hastigheten?

>>> harmonic_mean([40, 60], weights=[5, 30])
56.0

StatisticsError uppstår om data är tomt, om något element är mindre än noll eller om den viktade summan inte är positiv.

Den nuvarande algoritmen har en tidig utgång när den stöter på en nolla i indata. Detta innebär att de efterföljande inmatningarna inte testas för giltighet. (Detta beteende kan komma att ändras i framtiden)

Tillagd i version 3.6.

Ändrad i version 3.10: Lagt till stöd för vikter.

statistics.kde(data, h, kernel='normal', *, cumulative=False)

Kernel Density Estimation (KDE): Skapa en kontinuerlig sannolikhetstäthetsfunktion eller kumulativ fördelningsfunktion från diskreta prov.

Grundtanken är att jämna ut data med hjälp av en kärnfunktion. för att hjälpa till att dra slutsatser om en population från ett urval.

Graden av utjämning styrs av skalningsparametern h, som kallas bandbredd. Mindre värden framhäver lokala särdrag medan större värden ger ett jämnare resultat.

Kärnan bestämmer de relativa vikterna för datapunkterna i urvalet. I allmänhet har valet av kärnform inte lika stor betydelse som den mer inflytelserika parametern för utjämning av bandbredd.

Kärnor som ger viss vikt åt varje provpunkt inkluderar normal (gauss), logistisk och sigmoid.

Kärnor som bara ger vikt åt provpunkter inom bandbredden inkluderar rektangulär (uniform), triangulär, parabolisk (epanechnikov), kvadratisk (bivikt), trivikt och cosinus.

Om cumulative är true, returneras en kumulativ fördelningsfunktion.

Ett StatisticsError kommer att uppstå om data-sekvensen är tom.

Wikipedia har ett exempel där vi kan använda kde() för att generera och plotta en sannolikhetstäthetsfunktion som uppskattats från ett litet urval:

>>> sample = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
>>> f_hat = kde(sample, h=1.5)
>>> xarr = [i/100 for i in range(-750, 1100)]
>>> yarr = [f_hat(x) for x in xarr]

Punkterna i xarr och yarr kan användas för att göra en PDF-plott: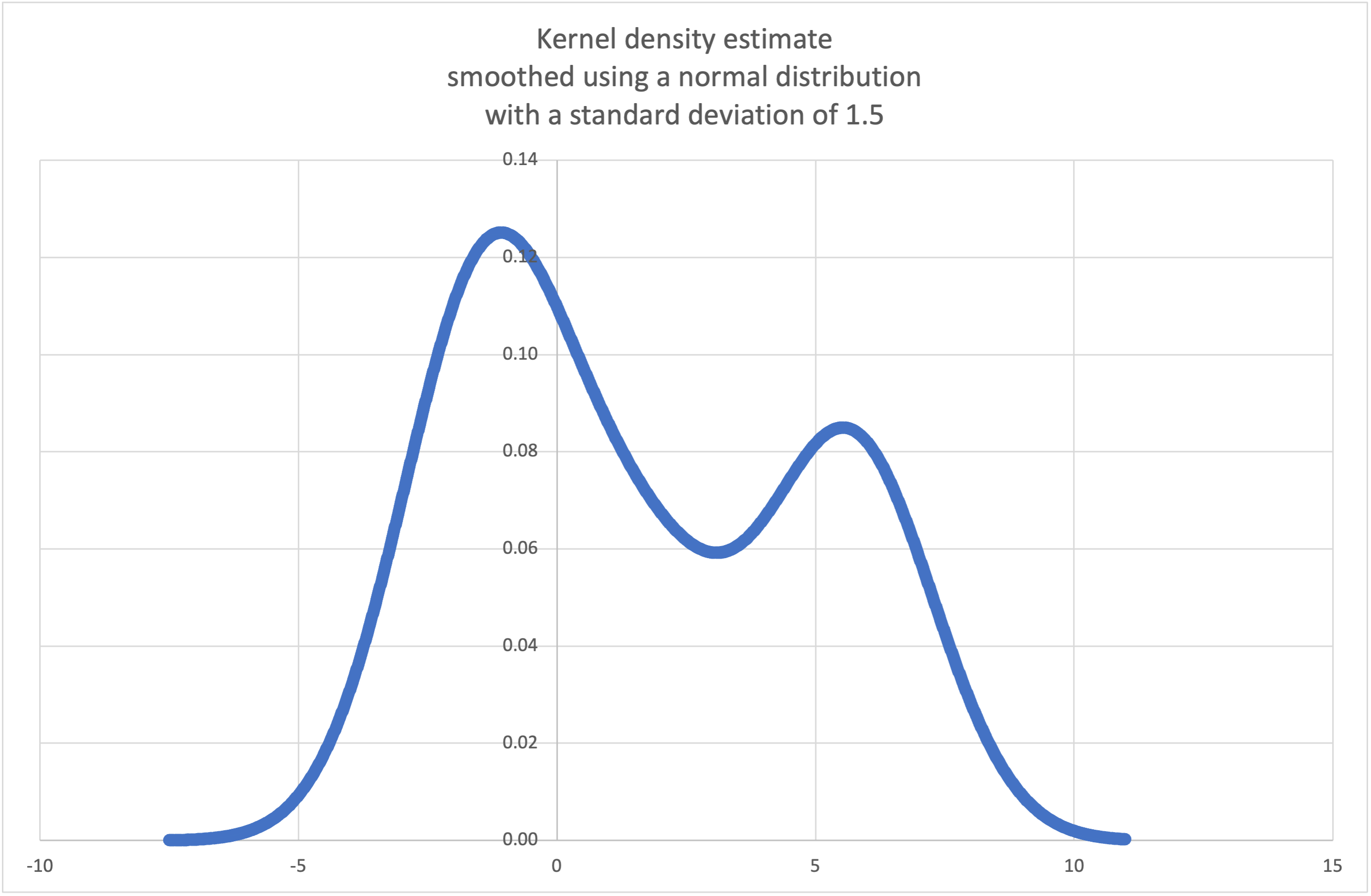

Tillagd i version 3.13.

statistics.kde_random(data, h, kernel='normal', *, seed=None)

Returnerar en funktion som gör ett slumpmässigt urval från den skattade sannolikhetstäthetsfunktionen som produceras av kde(data, h, kernel).

Genom att tillhandahålla ett frö möjliggörs reproducerbara urval. I framtiden kan värdena ändras något i takt med att mer exakta inversa CDF-estimat för kärnor implementeras. Seed kan vara ett heltal, float, str eller bytes.

Ett StatisticsError kommer att uppstå om data-sekvensen är tom.

Om vi fortsätter med exemplet för kde() kan vi använda kde_random() för att generera nya slumpmässiga val från en uppskattad sannolikhetstäthetsfunktion:

>>> data = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
>>> rand = kde_random(data, h=1.5, seed=8675309)
>>> new_selections = [rand() for i in range(10)]
>>> [round(x, 1) for x in new_selections]
[0.7, 6.2, 1.2, 6.9, 7.0, 1.8, 2.5, -0.5, -1.8, 5.6]

Tillagd i version 3.13.

statistics.median(data)

Returnerar medianen (mittvärdet) för numeriska data med hjälp av den vanliga metoden ”medelvärdet av de två mittersta”. Om data är tomt kommer StatisticsError att returneras. data kan vara en sekvens eller en iterabel.

Medianen är ett robust mått på central placering och påverkas mindre av förekomsten av avvikande värden. När antalet datapunkter är udda returneras den mittersta datapunkten:

>>> median([1, 3, 5])
3

När antalet datapunkter är jämnt interpoleras medianen genom att ta medelvärdet av de två mellersta värdena:

>>> median([1, 3, 5, 7])
4.0

Detta är lämpligt när dina data är diskreta och du inte bryr dig om att medianen kanske inte är en faktisk datapunkt.

Om data är ordinala (stöder orderoperationer) men inte numeriska (stöder inte addition) kan du överväga att använda median_low() eller median_high() i stället.

statistics.median_low(data)

Returnerar den låga medianen för numeriska data. Om data är tomt kommer StatisticsError att returneras. data kan vara en sekvens eller en iterabel.

Den låga medianen ingår alltid i datauppsättningen. När antalet datapunkter är udda returneras det mittersta värdet. Om det är jämnt returneras det minsta av de två mittvärdena.

>>> median_low([1, 3, 5])
3
>>> median_low([1, 3, 5, 7])
3

Använd den låga medianen när dina data är diskreta och du föredrar att medianen är en faktisk datapunkt snarare än interpolerad.

statistics.median_high(data)

Returnerar den höga medianen för data. Om data är tomt, StatisticsError tas upp. data kan vara en sekvens eller en iterabel.

Den höga medianen ingår alltid i datauppsättningen. När antalet datapunkter är udda returneras det mittersta värdet. Om det är jämnt returneras det största av de två mittvärdena.

>>> median_high([1, 3, 5])
3
>>> median_high([1, 3, 5, 7])
5

Använd den höga medianen när dina data är diskreta och du föredrar att medianen är en faktisk datapunkt snarare än interpolerad.

statistics.median_grouped(data, interval=1.0)

Beräknar medianen för numeriska data som har grupperats eller binnats runt mittpunkterna i på varandra följande intervall med fast bredd.

Data kan vara vilken iterabel som helst av numeriska data där varje värde är exakt mittpunkten i en bin. Åtminstone ett värde måste finnas.

Intervall är bredden på varje bin.

Demografisk information kan t.ex. ha sammanfattats i på varandra följande tioåriga åldersgrupper där varje grupp representeras av intervallens 5-åriga mittpunkter:

>>> from collections import Counter
>>> demographics = Counter({
...    25: 172,   # 20 to 30 years old
...    35: 484,   # 30 to 40 years old
...    45: 387,   # 40 to 50 years old
...    55:  22,   # 50 to 60 years old
...    65:   6,   # 60 to 70 years old
... })
...

Den 50:e percentilen (medianen) är den 536:e personen av de 1071 medlemmarna i kohorten. Den personen är i åldersgruppen 30 till 40 år.

Den vanliga funktionen median() skulle anta att alla i åldersgruppen tricenarianer var exakt 35 år gamla. Ett mer hållbart antagande är att de 484 medlemmarna i den åldersgruppen är jämnt fördelade mellan 30 och 40. För det använder vi median_grouped():

>>> data = list(demographics.elements())
>>> median(data)
35
>>> round(median_grouped(data, interval=10), 1)
37.5

Anroparen ansvarar för att datapunkterna är åtskilda med exakta multiplar av intervall. Detta är viktigt för att få ett korrekt resultat. Funktionen kontrollerar inte detta förhandsvillkor.

Ingångarna kan vara av vilken numerisk typ som helst som kan omvandlas till en float under interpoleringssteget.

statistics.mode(data)

Returnerar den enskilt vanligaste datapunkten från diskreta eller nominella data. Läget (när det finns) är det mest typiska värdet och fungerar som ett mått på central placering.

Om det finns flera lägen med samma frekvens returneras det första som påträffas i data. Om den minsta eller största av dessa önskas istället, använd min(multimode(data)) eller max(multimode(data)). Om indata data är tomt, kommer StatisticsError att visas.

mode förutsätter diskreta data och returnerar ett enda värde. Detta är standardbehandlingen av mode som vanligtvis lärs ut i skolorna:

>>> mode([1, 1, 2, 3, 3, 3, 3, 4])
3

Mode är unikt eftersom det är den enda statistiken i det här paketet som även gäller för nominella (icke-numeriska) data:

>>> mode(["red", "blue", "blue", "red", "green", "red", "red"])
'red'

Endast hashbara indata stöds. För att hantera typen set, överväg att casta till frozenset. För att hantera typen list, överväg att casta till tuple. För blandade eller nästlade indata kan du överväga att använda den här långsammare kvadratiska algoritmen som bara beror på likhetstester: max(data, key=data.count).

Ändrad i version 3.8: Hanterar nu multimodala dataset genom att returnera det första läget som påträffas. Tidigare gav den StatisticsError när mer än ett läge hittades.

statistics.multimode(data)

Returnerar en lista med de mest frekvent förekommande värdena i den ordning de först påträffades i data. Returnerar mer än ett resultat om det finns flera lägen eller en tom lista om data är tom:

>>> multimode('aabbbbccddddeeffffgg')
['b', 'd', 'f']
>>> multimode('')
[]

Tillagd i version 3.8.

statistics.pstdev(data, mu=None)

Returnerar populationens standardavvikelse (kvadratroten av populationens varians). Se pvariance() för argument och andra detaljer.

>>> pstdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75])
0.986893273527251

statistics.pvariance(data, mu=None)

Returnerar populationsvariansen för data, en icke-tom sekvens eller iterabel av realvärdesberäknade tal. Varians, eller andra momentet kring medelvärdet, är ett mått på variabiliteten (spridningen) i data. En stor varians indikerar att data är utspridda; en liten varians indikerar att de är grupperade tätt runt medelvärdet.

Om det valfria andra argumentet mu anges bör det vara populationens medelvärde för data. Det kan också användas för att beräkna det andra momentet runt en punkt som inte är medelvärdet. Om det saknas eller är None (standard) beräknas det aritmetiska medelvärdet automatiskt.

Använd denna funktion för att beräkna variansen från hela populationen. För att uppskatta variansen från ett urval är funktionen variance() vanligtvis ett bättre val.

Utlöser StatisticsError om data är tomt.

Exempel:

>>> data = [0.0, 0.25, 0.25, 1.25, 1.5, 1.75, 2.75, 3.25]
>>> pvariance(data)
1.25

Om du redan har beräknat medelvärdet för dina data kan du skicka det som det valfria andra argumentet mu för att undvika omberäkning:

>>> mu = mean(data)
>>> pvariance(data, mu)
1.25

Decimaler och bråk stöds:

>>> from decimal import Decimal as D
>>> pvariance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")])
Decimal('24.815')

>>> from fractions import Fraction as F
>>> pvariance([F(1, 4), F(5, 4), F(1, 2)])
Fraction(13, 72)

Anteckning

När detta kallas med hela populationen ger det populationsvariansen σ². När det i stället gäller ett urval är detta den partiska urvalsvariansen s², även känd som varians med N frihetsgrader.

Om du på något sätt känner till det sanna populationsmedelvärdet μ, kan du använda denna funktion för att beräkna variansen för ett urval, med det kända populationsmedelvärdet som andra argument. Förutsatt att datapunkterna är ett slumpmässigt urval av populationen blir resultatet en väntevärdesriktig skattning av populationsvariansen.

statistics.stdev(data, xbar=None)

Returnerar standardavvikelsen för urvalet (kvadratroten av variansen för urvalet). Se variance() för argument och andra detaljer.

>>> stdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75])
1.0810874155219827

statistics.variance(data, xbar=None)

Returnerar urvalsvariansen för data, en iterabel med minst två realvärdestal. Varians, eller andra momentet kring medelvärdet, är ett mått på variabiliteten (spridningen) i data. En stor varians indikerar att data är utspridda, medan en liten varians indikerar att de är grupperade tätt kring medelvärdet.

Om det valfria andra argumentet xbar anges bör det vara medelvärdet för data för provet. Om det saknas eller är None (standard) beräknas medelvärdet automatiskt.

Använd den här funktionen när dina data är ett urval från en population. För att beräkna variansen från hela populationen, se pvariance().

Utlöser StatisticsError om data har färre än två värden.

Exempel:

>>> data = [2.75, 1.75, 1.25, 0.25, 0.5, 1.25, 3.5]
>>> variance(data)
1.3720238095238095

Om du redan har beräknat urvalsmedelvärdet för dina data kan du skicka det som det valfria andra argumentet xbar för att undvika omräkning:

>>> m = mean(data)
>>> variance(data, m)
1.3720238095238095

Denna funktion försöker inte verifiera att du har angett det faktiska medelvärdet som xbar. Om du använder godtyckliga värden för xbar kan det leda till ogiltiga eller omöjliga resultat.

Decimal- och fraktionsvärden stöds:

>>> from decimal import Decimal as D
>>> variance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")])
Decimal('31.01875')

>>> from fractions import Fraction as F
>>> variance([F(1, 6), F(1, 2), F(5, 3)])
Fraction(67, 108)

Anteckning

Detta är urvalsvariansen s² med Bessels korrigering, även känd som varians med N-1 frihetsgrader. Förutsatt att datapunkterna är representativa (t.ex. oberoende och identiskt fördelade) bör resultatet vara en väntevärdesriktig skattning av den verkliga populationsvariansen.

Om du på något sätt känner till det faktiska populationsmedelvärdet μ bör du skicka det till funktionen pvariance() som parametern mu för att få variansen för ett urval.

statistics.quantiles(data, *, n=4, method='exclusive')

Dela upp data i n kontinuerliga intervall med samma sannolikhet. Returnerar en lista med n - 1 skärningspunkter som separerar intervallen.

Ställ in n på 4 för kvartiler (standard). Ställ in n till 10 för deciler. Ställ in n på 100 för percentiler, vilket ger de 99 snittpunkter som delar in data i 100 lika stora grupper. Utlöser StatisticsError om n inte är minst 1.

data kan vara vilken iterabel som helst som innehåller exempeldata. För meningsfulla resultat bör antalet datapunkter i data vara större än n. Utlöser StatisticsError om det inte finns minst en datapunkt.

Skärningspunkterna interpoleras linjärt från de två närmaste datapunkterna. Om en skärningspunkt t.ex. ligger en tredjedel av avståndet mellan två provvärden, 100 och 112, kommer skärningspunkten att utvärderas till 104.

Metoden för att beräkna kvantiler kan varieras beroende på om data inkluderar eller exkluderar de lägsta och högsta möjliga värdena från populationen.

Standardmetoden method är ”exclusive” och används för data som samlats in från en population som kan ha mer extrema värden än vad som finns i urvalet. Den del av populationen som faller under i-th av m sorterade datapunkter beräknas som i / (m + 1). Med nio urvalsvärden sorterar metoden dem och tilldelar följande percentiler: 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%.

Om method är inställd på ”inclusive” används den för att beskriva populationsdata eller för stickprov som man vet innehåller de mest extrema värdena från populationen. Minimivärdet i data behandlas som den 0:e percentilen och maximivärdet behandlas som den 100:e percentilen. Den del av populationen som faller under i-th av m sorterade datapunkter beräknas som (i - 1) / (m - 1). Givet 11 provvärden sorterar metoden dem och tilldelar följande percentiler: 0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, 100%.

# Decile cut points for empirically sampled data
>>> data = [105, 129, 87, 86, 111, 111, 89, 81, 108, 92, 110,
...         100, 75, 105, 103, 109, 76, 119, 99, 91, 103, 129,
...         106, 101, 84, 111, 74, 87, 86, 103, 103, 106, 86,
...         111, 75, 87, 102, 121, 111, 88, 89, 101, 106, 95,
...         103, 107, 101, 81, 109, 104]
>>> [round(q, 1) for q in quantiles(data, n=10)]
[81.0, 86.2, 89.0, 99.4, 102.5, 103.6, 106.0, 109.8, 111.0]

Tillagd i version 3.8.

Ändrad i version 3.13: Det uppstår inte längre något undantag för en indata med endast en enda datapunkt. Detta gör att kvantilskattningar kan byggas upp med en provpunkt i taget och gradvis bli mer förfinade med varje ny datapunkt.

statistics.covariance(x, y, /)

Returnerar sampelkovariansen för två indata x och y. Kovarians är ett mått på den gemensamma variabiliteten hos två indata.

Båda inmatningarna måste vara lika långa (inte mindre än två), annars StatisticsError tas upp.

Exempel:

>>> x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> y = [1, 2, 3, 1, 2, 3, 1, 2, 3]
>>> covariance(x, y)
0.75
>>> z = [9, 8, 7, 6, 5, 4, 3, 2, 1]
>>> covariance(x, z)
-7.5
>>> covariance(z, x)
-7.5

Tillagd i version 3.10.

statistics.correlation(x, y, /, *, method='linear')

Returnerar Pearsons korrelationskoefficient för två indata. Pearsons korrelationskoefficient r tar värden mellan -1 och +1. Den mäter styrkan och riktningen i ett linjärt förhållande.

Om method är ”ranked”, beräknas Spearmans rangkorrelationskoefficient för två indata. Data ersätts av rangordningar. Oavgjorda värden får ett genomsnitt så att lika värden får samma rangordning. Den resulterande koefficienten mäter styrkan i ett monotont förhållande.

Spearmans korrelationskoefficient är lämplig för ordinaldata eller för kontinuerliga data som inte uppfyller kravet på linjär proportion för Pearsons korrelationskoefficient.

Båda indata måste vara lika långa (minst två), och behöver inte vara konstanta, annars StatisticsError tas upp.

Exempel med Kepler’s lagar för planetrörelse:

>>> # Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and  Neptune
>>> orbital_period = [88, 225, 365, 687, 4331, 10_756, 30_687, 60_190]    # days
>>> dist_from_sun = [58, 108, 150, 228, 778, 1_400, 2_900, 4_500] # million km

>>> # Show that a perfect monotonic relationship exists
>>> correlation(orbital_period, dist_from_sun, method='ranked')
1.0

>>> # Observe that a linear relationship is imperfect
>>> round(correlation(orbital_period, dist_from_sun), 4)
0.9882

>>> # Demonstrate Kepler's third law: There is a linear correlation
>>> # between the square of the orbital period and the cube of the
>>> # distance from the sun.
>>> period_squared = [p * p for p in orbital_period]
>>> dist_cubed = [d * d * d for d in dist_from_sun]
>>> round(correlation(period_squared, dist_cubed), 4)
1.0

Tillagd i version 3.10.

Ändrad i version 3.12: Stöd för Spearmans rangkorrelationskoefficient har lagts till.

statistics.linear_regression(x, y, /, *, proportional=False)

Returnerar lutningen och interceptet för parametrar för enkel linjär regression som uppskattats med hjälp av vanliga minsta kvadratmetoden. Enkel linjär regression beskriver förhållandet mellan en oberoende variabel x och en beroende variabel y i termer av denna linjära funktion:

y = lutning * x + intercept + brus

där slope och intercept är de regressionsparametrar som uppskattas, och noise representerar variationen i data som inte förklaras av den linjära regressionen (det är lika med skillnaden mellan förutsagda och faktiska värden för den beroende variabeln).

Båda indata måste vara lika långa (minst två) och den oberoende variabeln x får inte vara konstant, annars uppstår ett StatisticsError.

Vi kan till exempel använda premiärdatum för Monty Python-filmerna” för att förutsäga det kumulativa antalet Monty Python-filmer som skulle ha producerats fram till 2019, förutsatt att de hade hållit samma takt.

>>> year = [1971, 1975, 1979, 1982, 1983]
>>> films_total = [1, 2, 3, 4, 5]
>>> slope, intercept = linear_regression(year, films_total)
>>> round(slope * 2019 + intercept)
16

Om proportional är sant antas den oberoende variabeln x och den beroende variabeln y vara direkt proportionella. Data anpassas till en linje som går genom origo. Eftersom skärningspunkten alltid kommer att vara 0,0 förenklas den underliggande linjära funktionen till:

y = lutning * x + brus

Vi fortsätter med exemplet från correlation() och undersöker hur väl en modell som baseras på större planeter kan förutsäga omloppsavståndet för dvärgplaneter:

>>> model = linear_regression(period_squared, dist_cubed, proportional=True)
>>> slope = model.slope

>>> # Dwarf planets:   Pluto,  Eris,    Makemake, Haumea, Ceres
>>> orbital_periods = [90_560, 204_199, 111_845, 103_410, 1_680]  # days
>>> predicted_dist = [math.cbrt(slope * (p * p)) for p in orbital_periods]
>>> list(map(round, predicted_dist))
[5912, 10166, 6806, 6459, 414]

>>> [5_906, 10_152, 6_796, 6_450, 414]  # actual distance in million km
[5906, 10152, 6796, 6450, 414]

Tillagd i version 3.10.

Ändrad i version 3.11: Stöd för proportionell har lagts till.

Undantag

Ett enda undantag definieras:

exception statistics.StatisticsError

Underklass till ValueError för statistikrelaterade undantag.

NormalDist objekt

NormalDist är ett verktyg för att skapa och manipulera normalfördelningar av en slumpmässig variabel. Det är en klass som behandlar medelvärdet och standardavvikelsen för datamätningar som en enda enhet.

Normalfördelningar härrör från Central Limit Theorem och har ett brett spektrum av tillämpningar inom statistik.

class statistics.NormalDist(mu=0.0, sigma=1.0)

Returnerar ett nytt NormalDist-objekt där mu representerar det aritmetiska medelvärdet och sigma representerar standardavvikelsen.

Om sigma är negativ, uppstår StatisticsError.

mean

En skrivskyddad egenskap för det aritmetiska medelvärdet för en normalfördelning.

median

En skrivskyddad egenskap för median för en normalfördelning.

mode

En skrivskyddad egenskap för mode för en normalfördelning.

stdev

En skrivskyddad egenskap för standardavvikelsen för en normalfördelning.

variance

En skrivskyddad egenskap för variansen i en normalfördelning. Lika med kvadraten på standardavvikelsen.

classmethod from_samples(data)

Skapar en normalfördelningsinstans med parametrarna mu och sigma uppskattade från data med hjälp av fmean() och stdev().

data kan vara valfri iterable och bör bestå av värden som kan konverteras till typen float. Om data inte innehåller minst två element, uppstår StatisticsError eftersom det krävs minst en punkt för att skatta ett centralt värde och minst två punkter för att skatta spridningen.

samples(n, *, seed=None)

Genererar n slumpmässiga stickprov för ett givet medelvärde och standardavvikelse. Returnerar en list av float-värden.

Om seed anges skapas en ny instans av den underliggande slumptalsgeneratorn. Detta är användbart för att skapa reproducerbara resultat, även i ett sammanhang med flera trådar.

Ändrad i version 3.13.

Bytte till en snabbare algoritm. För att återskapa exempel från tidigare versioner, använd random.seed() och random.gauss().

pdf(x)

Med hjälp av en sannolikhetstäthetsfunktion (pdf), beräkna den relativa sannolikheten för att en slumpmässig variabel X kommer att ligga nära det givna värdet x. Matematiskt sett är det gränsen för förhållandet P(x <= X < x+dx) / dx när dx närmar sig noll.

Den relativa sannolikheten beräknas som sannolikheten för att ett prov förekommer inom ett smalt område dividerat med områdets bredd (därav ordet ”densitet”). Eftersom sannolikheten är relativ i förhållande till andra punkter kan dess värde vara större än ”1,0”.

cdf(x)

Med hjälp av en cumulative distribution function (cdf), beräkna sannolikheten för att en slumpmässig variabel X kommer att vara mindre än eller lika med x. Matematiskt skrivs det P(X <= x).

inv_cdf(p)

Beräkna den inversa kumulativa fördelningsfunktionen, även känd som kvantielfunktionen eller procentpunktsfunktionen. Matematiskt skrivs den x : P(X <= x) = p.

Tar reda på värdet x för den slumpmässiga variabeln X så att sannolikheten för att variabeln är mindre än eller lika med detta värde är lika med den givna sannolikheten p.

overlap(other)

Mäter överensstämmelsen mellan två normala sannolikhetsfördelningar. Returnerar ett värde mellan 0,0 och 1,0 som anger överlappningsområdet för de två sannolikhetstäthetsfunktionerna.

quantiles(n=4)

Dela upp normalfördelningen i n kontinuerliga intervall med samma sannolikhet. Returnerar en lista med (n - 1) skärningspunkter som separerar intervallen.

Ställ in n på 4 för kvartiler (standard). Ställ in n till 10 för deciler. Ställ in n på 100 för percentiler, vilket ger de 99 skärningspunkter som delar upp normalfördelningen i 100 lika stora grupper.

zscore(x)

Beräkna Standardpoäng som beskriver x i termer av antalet standardavvikelser över eller under normalfördelningens medelvärde: (x - mean) / stdev.

Tillagd i version 3.9.

Instanser av NormalDist stöder addition, subtraktion, multiplikation och division med en konstant. Dessa operationer används för översättning och skalning. Ett exempel:

>>> temperature_february = NormalDist(5, 2.5)             # Celsius
>>> temperature_february * (9/5) + 32                     # Fahrenheit
NormalDist(mu=41.0, sigma=4.5)

Att dividera en konstant med en instans av NormalDist stöds inte eftersom resultatet inte skulle vara normalfördelat.

Eftersom normalfördelningar uppstår genom additiva effekter av oberoende variabler, är det möjligt att addera och subtrahera två oberoende normalfördelade slumpmässiga variabler representerade som instanser av NormalDist. Till exempel:

>>> birth_weights = NormalDist.from_samples([2.5, 3.1, 2.1, 2.4, 2.7, 3.5])
>>> drug_effects = NormalDist(0.4, 0.15)
>>> combined = birth_weights + drug_effects
>>> round(combined.mean, 1)
3.1
>>> round(combined.stdev, 1)
0.5

Tillagd i version 3.8.

Exempel och recept

Klassiska sannolikhetsproblem

NormalDist löser enkelt klassiska sannolikhetsproblem.

Om du till exempel har historiska data för SAT-prov som visar att resultaten är normalfördelade med ett medelvärde på 1060 och en standardavvikelse på 195, kan du bestämma andelen elever med provresultat mellan 1100 och 1200, efter avrundning till närmaste heltal:

>>> sat = NormalDist(1060, 195)
>>> fraction = sat.cdf(1200 + 0.5) - sat.cdf(1100 - 0.5)
>>> round(fraction * 100.0, 1)
18.4

Hitta kvartilerna och decilerna för SAT-poängen:

>>> list(map(round, sat.quantiles()))
[928, 1060, 1192]
>>> list(map(round, sat.quantiles(n=10)))
[810, 896, 958, 1011, 1060, 1109, 1162, 1224, 1310]

Monte Carlo-ingångar för simuleringar

För att uppskatta fördelningen för en modell som inte är lätt att lösa analytiskt kan NormalDist generera indataprov för en Monte Carlo-simulering:

>>> def model(x, y, z):
...     return (3*x + 7*x*y - 5*y) / (11 * z)
...
>>> n = 100_000
>>> X = NormalDist(10, 2.5).samples(n, seed=3652260728)
>>> Y = NormalDist(15, 1.75).samples(n, seed=4582495471)
>>> Z = NormalDist(50, 1.25).samples(n, seed=6582483453)
>>> quantiles(map(model, X, Y, Z))
[1.4591308524824727, 1.8035946855390597, 2.175091447274739]

Approximation av binomialfördelningar

Normalfördelningar kan användas för att approximera binomialfördelningar när urvalsstorleken är stor och när sannolikheten för ett lyckat försök är nära 50%.

Till exempel har en konferens om öppen källkod 750 deltagare och två rum med en kapacitet på 500 personer. Det finns ett föredrag om Python och ett annat om Ruby. Vid tidigare konferenser föredrog 65% of av deltagarna att lyssna på Python-samtal. Om vi antar att deltagarnas preferenser inte har ändrats, hur stor är sannolikheten att Python-rummet håller sig inom kapacitetsgränserna?

>>> n = 750             # Sample size
>>> p = 0.65            # Preference for Python
>>> q = 1.0 - p         # Preference for Ruby
>>> k = 500             # Room capacity

>>> # Approximation using the cumulative normal distribution
>>> from math import sqrt
>>> round(NormalDist(mu=n*p, sigma=sqrt(n*p*q)).cdf(k + 0.5), 4)
0.8402

>>> # Exact solution using the cumulative binomial distribution
>>> from math import comb, fsum
>>> round(fsum(comb(n, r) * p**r * q**(n-r) for r in range(k+1)), 4)
0.8402

>>> # Approximation using a simulation
>>> from random import seed, binomialvariate
>>> seed(8675309)
>>> mean(binomialvariate(n, p) <= k for i in range(10_000))
0.8406

Naiv bayesiansk klassificerare

Normalfördelningar är vanligt förekommande i maskininlärningsproblem.

Wikipedia har ett trevligt exempel på en Naive Bayesian Classifier. Utmaningen är att förutsäga en persons kön från mätningar av normalfördelade egenskaper, inklusive längd, vikt och fotstorlek.

Vi får en träningsdatauppsättning med mätningar för åtta personer. Måtten antas vara normalfördelade, så vi sammanfattar data med NormalDist:

>>> height_male = NormalDist.from_samples([6, 5.92, 5.58, 5.92])
>>> height_female = NormalDist.from_samples([5, 5.5, 5.42, 5.75])
>>> weight_male = NormalDist.from_samples([180, 190, 170, 165])
>>> weight_female = NormalDist.from_samples([100, 150, 130, 150])
>>> foot_size_male = NormalDist.from_samples([12, 11, 12, 10])
>>> foot_size_female = NormalDist.from_samples([6, 8, 7, 9])

Därefter möter vi en ny person vars funktionsmätningar är kända men vars kön är okänt:

>>> ht = 6.0        # height
>>> wt = 130        # weight
>>> fs = 8          # foot size

Med utgångspunkt från en 50% prior sannolikhet för att vara man eller kvinna, beräknar vi posterior som prior gånger produkten av sannolikheter för funktionsmätningarna med tanke på kön:

>>> prior_male = 0.5
>>> prior_female = 0.5
>>> posterior_male = (prior_male * height_male.pdf(ht) *
...                   weight_male.pdf(wt) * foot_size_male.pdf(fs))

>>> posterior_female = (prior_female * height_female.pdf(ht) *
...                     weight_female.pdf(wt) * foot_size_female.pdf(fs))

Den slutliga prediktionen går till den största posterior. Detta kallas för maximal a posteriori eller MAP:

>>> 'male' if posterior_male > posterior_female else 'female'
'female'